Совершенствование методики оценки силовых воздействий на конструкцию длиннобазной железнодорожной платформы при перевозке контейнеров

Совершенствование методики оценки силовых воздействий на конструкцию длиннобазной железнодорожной платформы при перевозке контейнеров

За последние несколько лет на железных дорогах России и стран СНГ в эксплуатацию поступили новые модели длиннобазных платформ погрузочной длиной 24 метра (80 футов) для перевозки крупнотоннажных контейнеров, что было вызвано ростом объемов перевозок 12-метровых (40-футовых) контейнеров [1]. Вместе с тем при проектировании и постановке на производство новых конструкций вагонов разработчикам необходимо получить нагрузки на конструкцию, как на этапе выбора параметров, так и на этапе испытаний. Однако, как показал анализ нормативных документов по расчету и проектированию вагонов, а также технических требований к погрузке контейнеров, в настоящее время не выработаны однозначные рекомендации по расчетным и испытательным нагрузкам для специфических конструкций контейнерных платформ.

Основные эксплуатационные характеристики вагона, такие как грузоподъемность, эксплуатационная надежность и себестоимость, во многом определяются на этапе выбора параметров конструкции. Одним из основных критериев является прочность. Поэтому от полноты и достоверности информации о нагрузках, действующих на конструкцию, зависит технический уровень проекта в целом. В то же время ряд силовых воздействий на вагон от перевозимого контейнера в нормативных документах изложен в общей форме и требует дополнительной конкретизации. Для получения уточненных значений расчетных нагрузок от контейнеров и способа их приложения к конструкции вагона-платформы необходимо проведение расширенного анализа возможных схем установки контейнеров, а также определение статических и динамических воздействий на конструкцию длиннобазной платформы в эксплуатации.

Современные методы проектирования вагонов используют программные пакеты для конечно-элементного анализа конструкции. Применение такого инженерного инструмента позволяет увеличить точность расчетов прочности и жесткости конструкции, определения частот и форм колебаний, а также потери устойчивости формы. При этом для повышения общей точности определения перечисленных показателей необходимо уточнение расчетных нагрузок на конструкцию.

Таким образом, для решения задачи выбора параметров рамы длиннобазной контейнерной платформы с высокими прочностными характеристиками и минимальной массой тары актуальной является задача разработки уточненной методики приложения нагрузок от перевозимых контейнеров к конструкции платформы. Такая методика может быть использована при расчетах и испытаниях для обоснования нагрузок.

При разработке методики специалистами Инженерного центра был сформирован перечень эксплуатационных режимов железнодорожной платформы, определяющих нагрузки на конструкцию, выполнен обзор массовых и габаритных характеристик крупнотоннажных контейнеров, перевозимых железнодорожным транспортом, проведены вариантные расчеты изгибающих моментов в раме платформы от вертикальной статической нагрузки, создаваемой весом контейнеров. Кроме того, было проанализировано перераспределение сил между упорами крепления контейнеров при действии продольных ударных нагрузок и обобщены экспериментальные и расчетные данные о динамических нагрузках на платформу при движении с различными скоростями.

При определении нагрузок от перевозимого груза на конструкцию вагона-платформы наибольший интерес представляют силы, приводящие к наибольшим повреждающим воздействиям и являющиеся определяющими при выборе прочностных и жесткостных характеристик. Для контейнерной платформы основными режимами являются статическая нагрузка, динамическая нагрузка при соударении, а также вертикальные динамические нагрузки при движении.

Традиционно нагрузки на конструкцию объединены в несколько режимов, моделирующих сходные физические воздействия [2]. В большинстве случаев I и III режимы действия нагрузок рассматриваются как основные и обоснование параметров конструкции производят именно для них. Ремонтные нагрузки и нагрузки для расчета усталостной прочности используют для проверки уже сформированной конструкции. В то же время, применяя традиционный итерационный метод выбора параметров элементов конструкции, целесообразно в первую очередь прикладывать нагрузки, приводящие к наибольшим повреждающим воздействиям. В связи с этим в данной работе, кроме определенных в нормативных документах I и III режимов, как отдельные равнозначные режимы классифицированы ремонтные нагрузки и нагрузки для определения выполнения условий усталостной прочности (табл. 1).

Предложенный Инженерным центром подход к рассмотрению всех четырех режимов как равнозначных позволяет достоверно определять параметры конструкции на основании всего множества нагрузок.

Все нагрузки, действующие на конструкцию вагона-платформы, можно рассматривать как их множество. Несколько нагрузок, действующих одновременно, образуют сочетание нагрузок. Для каждого элемента или характерной зоны конструкции можно выделить множество сочетаний нагрузок, приводящих к наиболее опасным состояниям конструкции по критериям прочности, усталостной прочности и жесткости. Критерии, по которым оценивается конструкция, принимают экстремальные (максимальные или минимальные) значения при ограниченном количестве сочетаний нагрузок. Поэтому в данной работе было введено обозначение этих сочетаний нагрузок как лимитирующих.

Для решения задачи выбора параметров элементов конструкции разработан и рекомендован для использования алгоритм, в соответствии с которым на первом этапе моделирование нагруженного состояния проводится в соответствии с лимитирующим сочетанием нагрузок для исследуемой зоны. После окончания выбора параметров конструкции производится проверочный расчет для всех сочетаний нагрузок. Использование лимитирующих сочетаний нагрузок позволяет уменьшить количество расчетных моделей при решении задачи выбора параметров элементов конструкции.

Общеизвестно, что нагрузки на конструкцию платформы создаются перевозимым грузом – крупнотоннажными контейнерами. Основное распространение получили контейнеры длиной 20 и 40 футов [3]. В небольшом количестве (до 0,5%) по железным дорогам перевозят 30-футовые контейнеры. В последнее время ОАО «РЖД» рассматривало вопрос о возможности перевозок 45-футовых контейнеров, широко используемых в Северной Америке и вследствие процессов глобализации попадающих в транспортную систему России. Размеры и максимальная масса крупнотоннажных контейнеров соответствуют российским и международным стандартам (табл. 2) [7].

Следует отметить, что фактическая масса перевозимого контейнера, как правило, меньше максимально допускаемой. Так, средний вес груженого 20-футового контейнера составляет 16,5–18,8 тонны [5].

Практика проектирования вагоностроительными заводами совместно с Инженерным центром длиннобазных платформ показала, что особенностью эксплуатационных нагрузок на раму является большое количество используемых схем погрузки контейнеров. При выборе параметров элементов конструкции разработчику необходимо последовательно перебирать все варианты нагрузок для определения геометрических характеристик каждого элемента. Альтернативным решением явилось определение для каждой характерной зоны конструкции одного или нескольких лимитирующих сочетаний нагрузок, и, следовательно, возможных схем погрузки контейнеров, для которых были даны соответствующие им эпюры изгибающих моментов в раме вагона-платформы (табл. 3).

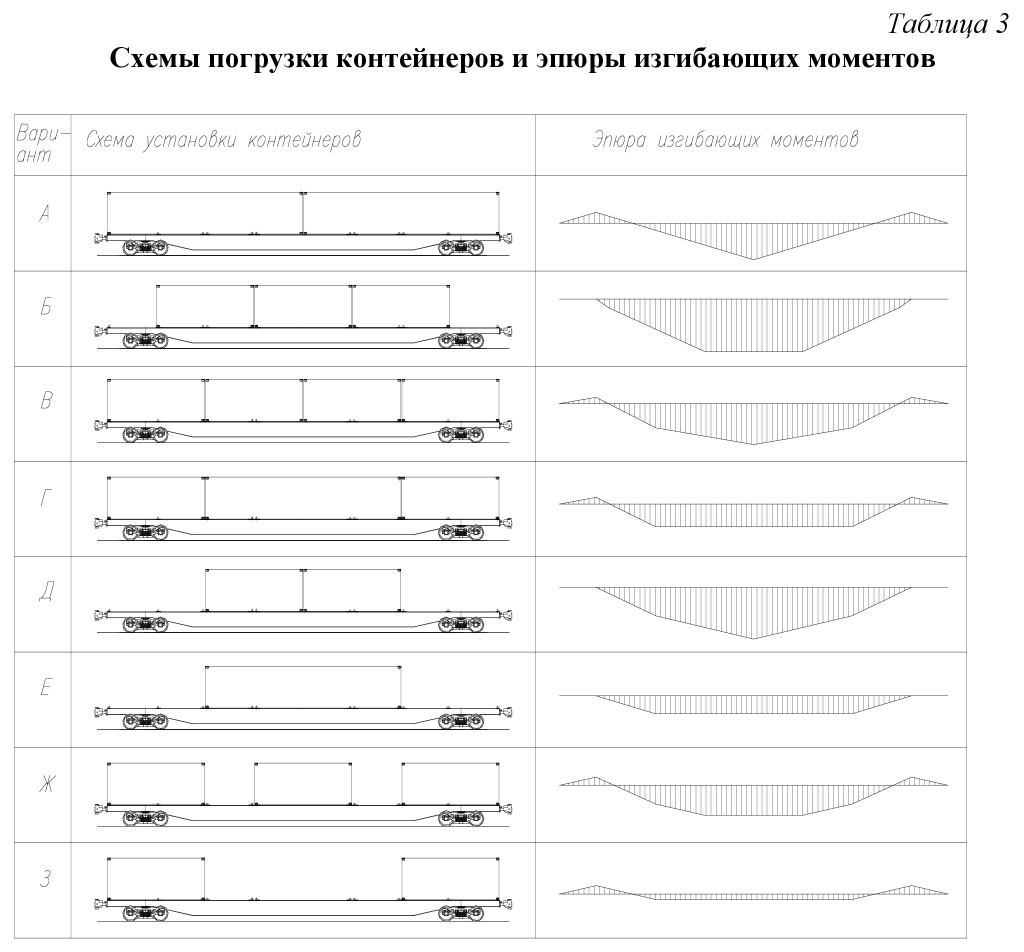
Приведенные эпюры наглядно демонстрируют, что можно выделить схемы погрузки, создающие наибольшие изгибающие моменты в характерных сечениях рамы. В качестве таких сечений были приняты: середина рамы, ось шкворневой балки, а также расстояние 1/4 длины базы от середины (рис. 1).

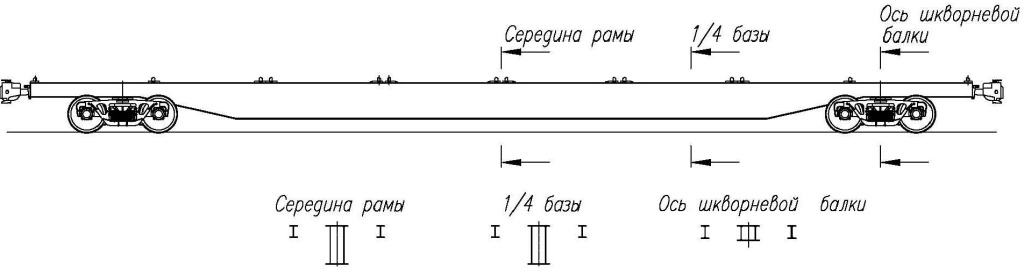Рис. 1. Схема контрольных сечений

Выбор сечений, произведенный на основе анализа наиболее распространенных конструкций платформ, позволяет определить характеристики основных несущих балок рамы. Изгибающие моменты в контрольных сечениях для каждой схемы погрузки контейнеров показаны на диаграмме (рис. 2).

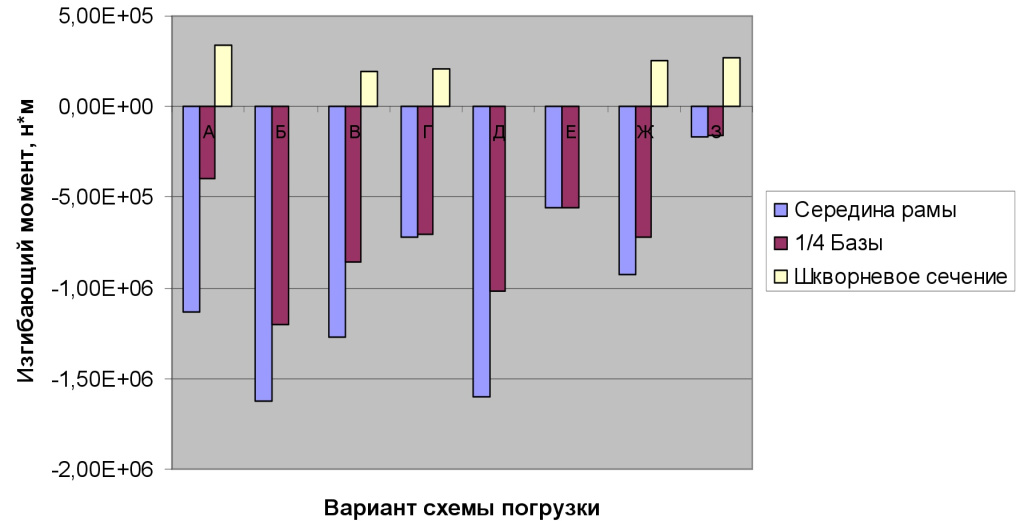Рис. 2. Изгибающие моменты при различных схемах погрузки контейнеров

На основании проведенного сравнительного анализа выявлены схемы действия нагрузок, при которых в конструкции возникают наибольшие напряжения и прогибы как следствие максимальных изгибающих моментов. Таким образом, при определении параметров средней части рамы разработчику конструкции целесообразно использовать нагружение по схеме А, Б иди Д (см. табл. 3) в зависимости от типа перевозимых контейнеров. Наибольшие нагрузки на консольную часть рамы и шкворневой узел возникают при нагружении по схеме А. Использование приведенных рекомендаций позволяет снизить число расчетных моделей и получить заведомо максимальные нагрузки при испытаниях.

Особенности конструкции вагона-платформы и специфика установки и крепления перевозимых контейнеров определили необходимость исследования распределения сил от груза, действующих на конструкцию при динамических воздействиях на вагон в целом. Необходимо учитывать перераспределение вертикальной нагрузки от контейнеров при действии продольных динамических сил (рис. 3).

Вертикальные составляющие силы веса контейнера, действующие на передние и задние упоры F_y1 и F_y2 соответственно, при действии ускорения вдоль оси х (продольной оси вагона) могут быть определены по следующим формулам:

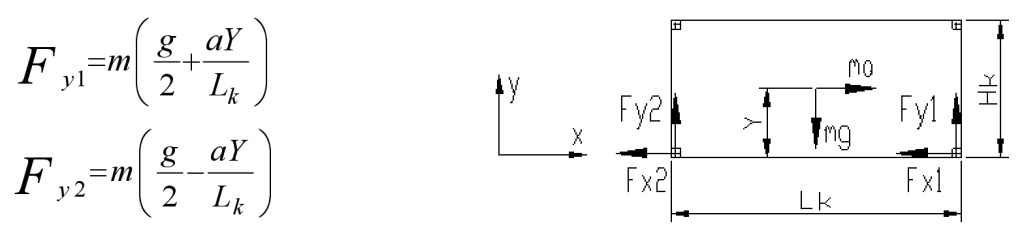Рис. 3. Схема действия сил на контейнер

Полученные зависимости позволяют определять расчетные значения динамических надбавок при моделировании продольных динамических нагрузок. Проведенные расчеты дополнительных нагрузок от клевка контейнера показали значение динамической добавки до 70% статической силы для 40-футовых контейнеров и до 80% для 20-футовых. Учет приведенных добавок существенно увеличил нагрузку на консольную часть рамы платформы и позволил выбрать размеры балок, обеспечивающие эксплуатационную надежность. Обоснованность полученных результатов была подтверждена результатами испытаний на прочность при соударении. Испытания проводились с загрузкой 20- и 40-футовых контейнеров. Зафиксированные динамические напряжения в консольной части хребтовой и боковых балок показали хорошую сходимость с расчетными значениями.

При движении вагона возникают динамические силы, направленные в вертикальной плоскости [6]. Соотношение динамической силы к статической принято обозначать как коэффициент динамики (К_дв). Для определения динамической нагруженности конструкции вагона используют методику приложения квазистатических сил. Для определения значений этих сил, как правило, получают значение напряжения для статической нагрузки и определяют динамическую нагрузку по следующей формуле:

F_дин=F_стат ×K_дв.

Таким образом, для определения значений динамических сил разработчику необходимо получить значение коэффициента вертикальной динамики. Зависимость коэффициента вертикальной динамики от скорости движения вагона, приведенная в нормативных документах, изначально была получена специалистами ВНИИЖТа и ГОСНИИВа [7] для подвижного состава меньшей длины, чем новые длиннобазные платформы. Уже при испытаниях платформ с длиной базы 14–15 метров испытательными центрами были получены результаты, потребовавшие введения дополнительной поправки в формулу расчета коэффициента динамики.

При испытании платформ с длинной базой 18–20 м Испытательным центром Инженерного центра и другими испытательными центрами также были получены значения динамических напряжений, что позволило произвести сравнение значений коэффициентов динамики для различных зон рамы платформы с полученными по аналитической зависимости. Испытания проводились во всем диапазоне эксплуатационных скоростей. Была исследована динамическая нагруженность рамы в середине длины, в зоне шкворневой балки и на расстоянии ¼ длины базы от середины (рис. 4).

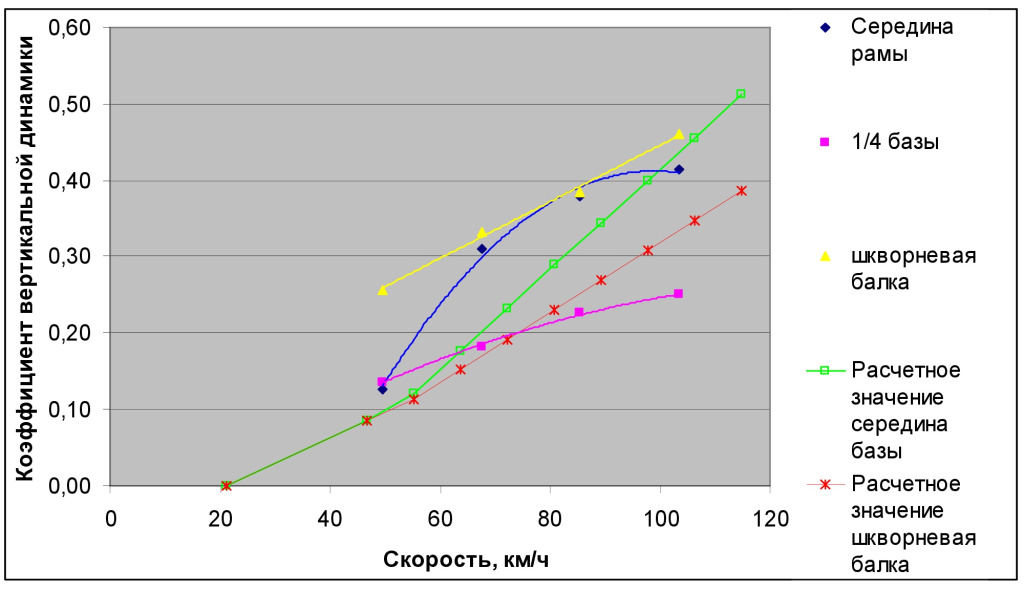  Рис. 4. Зависимость коэффициента вертикальной динамики от скорости

Сравнение результатов испытаний и аналитической зависимости показывает, что динамические напряжения в раме платформы на 20–25% превышают расчетные. Такое превышение особенно заметно в интервале скоростей 70–90 км/ч, что и может вносить существенную поправку в расчет сопротивления усталости. Проведенные испытания показывают, что используемые в настоящее время расчетные зависимости требуют уточнения для повышения точности расчетов прочности и сопротивления усталости длиннобазных платформ.

Таким образом, разработанная методика позволяют определить значения нагрузок и способ их приложения к конструкции вагона-платформы при расчетном обосновании выбора параметров. Было обосновано использование как I и III нормативных режимов нагружения, так и ремонтных нагрузок и нагрузок для расчета усталостной прочности в качестве равноценных при формировании множества расчетных нагрузок.

Показано, что можно определить схемы погрузки контейнеров, создающие наибольшие нагрузки на конструкцию. При определении параметров элементов конструкции можно ограничиться только этими схемами погрузки, так как выбранные параметры будут заведомо соответствовать остальным схемам. Такой подход позволяет снизить число вариантов расчетных нагрузок.

Проведенный анализ нагрузок на раму платформы от контейнеров при различных схемах установки позволил обосновать возможность определения лимитирующих расчетных случаев и осуществление выбора параметров конструкции в соответствии с ними, что позволяет снизить количество расчетных моделей.

Разработанная методика расчета перераспределения нагрузки от контейнеров при действии продольного ускорения позволила уточнить значения сил, прикладываемых к конструкции.

Сравнительный анализ коэффициентов вертикальной динамики, – полученных на испытаниях и по принятым в практике проектирования расчетным методикам, – показал необходимость уточнения аналитических зависимостей для более точного определения показателей динамической нагруженности длиннобазных контейнерных платформ.

Список литературы

1. Алексеева Ю. Новые фитинговые платформы выходят на рынок // Машины. Оборудование. Материалы. : прилож. к журн. «РЖД-Партнер». – 2006. – № 1. – С. 18–20.

2. Нормы для расчета и проектирования новых и модернизируемых вагонов железных дорог МПС колеи 1520 мм (несамоходных). М. : ГосНИИВ-ВНИИЖТ, 1996. – 316 с.

3. Перевозки крупнотоннажных контейнеров и автомобилей в сообщении Европа – Азия: справочник. – М. : Интекст, 1999. – 256 с.

4. ГОСТ 18477-79. Контейнеры универсальные. Типы, основные параметры и размеры. – М. : Изд-во стандартов, 1979. – 16 с.

5. http://www.rzd-partner.ru/news/?action=view&st=1158559203&id=1.

6. Соколов М. М. Динамическая нагруженность вагона / М. М. Соколов, В. Д. Хусидов, Ю. Г. Минкин. – М. : Транспорт, 1981. – С. 51–53.

7. Вагоны грузовые и пассажирские. Методы испытаний на прочность и ходовые качества : РД 24.050.37‑95. – М. : ГосНИИВ, 1995. – 102 с.

Содержание Сборники научных трудов